3D Mapping in Unstructured Environments

Background

The project with the full title “Learning of 3-Dimensional Maps of Unstructured Environments on a Mobile Robot” was funded by the Deutsche Forschungsgemeinschaft (DFG). It deals with the generation of 3D maps with a mobile robot in unstructured environments like search and rescue (SAR).

The DFG project lead to a very fast and robust form of mapping approach in form of 3D Plane SLAM that has been successfully used in different application scenarios. The project originally focused on Safety, Security, and Rescue Robotics (SSRR) as an application domain where the fast and robust generation of 3D maps is important [3][7][11]. But 3D Plane SLAM works surprisingly well in many unstructured environments including outdoor scenarios, e.g., in the context of planetary exploration [3][4][15] or underwater 3D mapping [10]. Furthermore, planar patches allow compact representations and they are well suited for computational geometry [9].

3D Plane SLAM

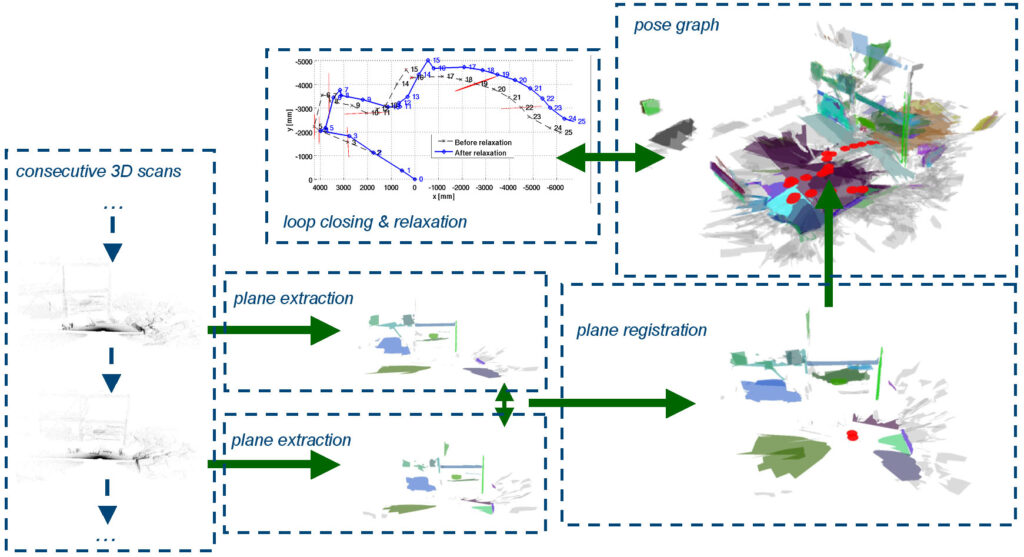
The mapping approach developed within this project consists of several steps

  1. consecutive acquisition of 3D range scans
  2. extraction of planes [2] including uncertainties [14]
  3. registration of scans based on plane sets [12]
  4. embedding of the registrations in a pose graph [5]
  5. loop detection and relaxation, i.e., 3D SLAM proper [11]

The different steps are also illustrated in the image on the right (click to enlarge). We are using different 3D range sensors for the first step including time of flight (TOF) cameras like PMD camera and Swissranger, stereo cameras, and self-made actuated laser range finders (aLRF). Some results within the project deal with the preprocessing of these data sources, e.g., to achieve sub-pixel accurary in TOF cameras [1] or to deal with the wrap-around error [8]. But most results are based on raw data from an aLRF in form of a SICK S300 that is rotation in a pitching motion by a simple servo. The main steps of the approach are short explained in the following.

Plane Extraction

After a scan is acquired, a set of planar-patches is extracted from the point-cloud that is associated with the related robot frame. Apart from the planar patch’s normal and distance to the origin, i.e., its defining parameters, the extraction procedure also gives their 4 x 4 covariance matrix. The plane extraction exploits the fact that a single 3D scan is based on 2.5D range measurements, the data can hence be treated as range images where an optimal fit in linear time is possible. In addition to the planes, their boundaries are extracted. The related polygons are not needed for the SLAM approach itself, the registration operates on the basic plane parameters. But the planes with their boundaries are the basis for the visualization and the actual usage of the 3D map. A description of the plane extraction can be found in [2]; the formal basis and the computation of the proper uncertainties is described in [14][6].

Plane Based Registration

The plane based registration is the core of 3D Plane SLAM. It works by

  • determining the correspondence set maximizing the global rigid body motion constraint
  • finding the optimal decoupled rotations (Wahba’s problem) and translations (closed form least squares) with related uncertainties

The core of the algorithm and a formal derivation of its principles are introduced in [12]. A detailed performance evaluation in comparison to the Iterative Closest Point (ICP) and the 3D Normal Distribution Transform (NDT) with a ground truth data-set is presented in [13]. The plane registration has several main advantages. First of all, it needs unlike any other approach to 3D SLAM no motion estimates from any other source like odometry, inertial navigation system, or similar, i.e., it is a global registration method. It hence still works under circumstances where other approaches fail, e.g., under large changes in 3D orientation (roll-pitch-yaw), low overlap between scans, many occlusions, or simply a combination of these challenges. Second, it is very fast and outperforms many other registration methods with respect to computation time.

Pose Graph SLAM

The plane registration presented in the previous section is in principle already suited for generating 3D maps by merging scans together. But though the errors are relatively small, they nevertheless accumulate and are hence in principle unbounded. It is therefore of interest to use proper Simultaneous Localization and Mapping (SLAM) for which the plane registration is fortunately particularly well suited for two main reasons. First of all, its theoretical basis allows for a proper determination of the uncertainties in the registration process. Second, theoretical analysis as well as practical experiment suggest that it is particularly robust with respect to rotations. The relaxation as result of loop closing in the SLAM can hence concentrate on translational errors for which an extremely fast closed form solution is possible [11].

Experiments and Results

3D Plane SLAM, respectively core elements of it like the plane registration have already been very successfully applied in different application scenarios. Several examples of high resolution 3D maps made with our method can be found on Youtube:

Bremen city center
http://www.youtube.com/watch?v=7sh-lLw5OdU
U-boot bunker Valentin
http://www.youtube.com/watch?v=Km1HhNa0Lh0
A search and rescue scenario
(including in addition 2D UAV-mapping)
http://www.youtube.com/watch?v=RKptRltPwo4

Further Links to 3D Datasets

Publications

Here some of the publications related to the project:

[1] K. Pathak, A. Birk, and J. Poppinga, “Sub-Pixel Depth Accuracy with a Time of Flight Sensor using Multimodal Gaussian Analysis,” in International Conference on Intelligent Robots and Systems (IROS), Nice, France, 2008. https://doi.org/10.1109/IROS.2008.4650841 [Preprint PDF]

[2] J. Poppinga, N. Vaskevicius, A. Birk, and K. Pathak, “Fast Plane Detection and Polygonalization in noisy 3D Range Images,” in International Conference on Intelligent Robots and Systems (IROS), Nice, France, 2008, pp. 3378 – 3383. https://doi.org/10.1109/IROS.2008.4650729 [Preprint PDF]

[3] A. Birk, S. Schwertfeger, and K. Pathak, “3D Data Collection at Disaster City at the 2008 NIST Response Robot Evaluation Exercise (RREE),” in IEEE International Workshop on Safety, Security, and Rescue Robotics (SSRR), Denver, 2009. https://doi.org/10.1109/SSRR.2009.5424164 [Preprint PDF]

[4] A. Birk, N. Vaskevicius, K. Pathak, S. Schwertfeger, J. Poppinga, and H. B{\”u}low, “3-D Perception and Modeling,” IEEE Robotics and Automation Magazine (RAM), special issue on Space Robotics, R. Wagner, R. Volpe, G. Visentin (Eds), vol. 6, pp. 53-60, December 2009. https://doi.org/10.1109/MRA.2009.934822 [Preprint PDF]

[5] K. Pathak, M. Pfingsthorn, N. Vaskevicius, and A. Birk, “Relaxing loop-closing errors in 3D maps based on planar surface patches,” in IEEE International Conference on Advanced Robotics (ICAR), 2009, pp. 1-6. [Preprint PDF]

[6] K. Pathak, N. Vaskevicius, and A. Birk, “Revisiting Uncertainty Analysis for Optimum Planes Extracted from 3D Range Sensor Point-Clouds,” in International Conference on Robotics and Automation (ICRA), 2009, pp. 1631 – 1636. https://doi.org/10.1109/ROBOT.2009.5152502 [Preprint PDF]

[7] K. Pathak, N. Vaskevicius, J. Poppinga, M. Pfingsthorn, S. Schwertfeger, and A. Birk, “Fast 3D Mapping by Matching Planes Extracted from Range Sensor Point-Clouds,” in International Conference on Intelligent Robots and Systems (IROS), 2009. https://doi.org/10.1109/IROS.2009.5354061 [Preprint PDF]

[8] J. Poppinga and A. Birk, “A Novel Approach to Wrap Around Error Correction for a Time-Of-Flight 3D Camera,” in RoboCup 2008: Robot WorldCup XII, Lecture Notes in Artificial Intelligence (LNAI). vol. 5399, L. Iocchi, H. Matsubara, A. Weitzenfeld, and C. Zhou, Eds., ed: Springer, 2009, pp. 247-258. https://doi.org/10.1007/978-3-642-02921-9_22 [Preprint PDF]

[9] A. Birk, K. Pathak, N. Vaskevicius, M. Pfingsthorn, J. Poppinga, and S. Schwertfeger, “Surface Representations for 3D Mapping: A Case for a Paradigm Shift,” KI – Kunstliche Intelligenz, vol. 24, pp. 249-254, 2010. https://doi.org/10.1007/s13218-010-0035-1 [Preprint PDF]

[10] K. Pathak, A. Birk, and N. Vaskevicius, “Plane-Based Registration of Sonar Data for Underwater 3D Mapping,” in IEEE International Conference on Intelligent Robots and Systems (IROS), Taipeh, Taiwan, 2010, pp. 4880 – 4885. https://doi.org/10.1109/IROS.2010.5650953 [Preprint PDF]

[11] K. Pathak, A. Birk, N. Vaskevicius, M. Pfingsthorn, S. Schwertfeger, and J. Poppinga, “Online 3D SLAM by Registration of Large Planar Surface Segments and Closed Form Pose-Graph Relaxation,” Journal of Field Robotics, Special Issue on 3D Mapping, vol. 27, pp. 52-84, 2010. https://doi.org/10.1002/rob.20322 [Preprint PDF]

[12] K. Pathak, A. Birk, N. Vaskevicius, and J. Poppinga, “Fast Registration Based on Noisy Planes with Unknown Correspondences for 3D Mapping,” IEEE Transactions on Robotics, vol. 26, pp. 424-441, 2010. https://doi.org/10.1109/TRO.2010.2042989 [Preprint PDF]

[13] K. Pathak, D. Borrmann, J. Elseberg, N. Vaskevicius, A. Birk, and A. Nuchter, “Evaluation of the Robustness of Planar-Patches based 3D-Registration using Marker-based Ground-Truth in an Outdoor Urban Scenario,” in International Conference on Intelligent Robots and Systems (IROS), Taipeh, Taiwan, 2010, pp. 5725 – 5730. https://doi.org/10.1109/IROS.2010.5649648 [Preprint PDF]

[14] K. Pathak, N. Vaskevicius, and A. Birk, “Uncertainty Analysis for Optimum Plane Extraction from Noisy 3D Range-Sensor Point-Clouds,” Intelligent Service Robotics, vol. 3, pp. 37–48, 2010. https://doi.org/10.1007/s11370-009-0057-4 [Preprint PDF]

[15] N. Vaskevicius, A. Birk, K. Pathak, S. Schwertfeger, and R. Rathnam, “Efficient Representation in 3D Environment Modeling for Planetary Robotic Exploration,” Advanced Robotics, vol. 24, pp. 1169-1197, 2010. https://doi.org/10.1163/016918610X501291 [Preprint PDF]